Publication Journal articles

많은 과학자 및 공학자들이 최근 주목하고 있는 인공지능 (artificial intelligent) 및 기계학습 (machine learning) 분야는 분석을 위해 많은 양의 데이터가 필요하고, 이를 정제해야 한다. 현재의 컴퓨터 아키텍처 (architecture)는 메모리 (memory)와 프로세서 (processor)가 구분되어 있고 버스 (bus)를 통해 데이터를 주고 받는데, 두 소자가 데이터에 접근하는 속도가 각각 달라서 대용량의 데이터를 처리할 때 속도에 문제가 생긴다. 이러한 현상을 ‘폰 노이만 병목현상’ (von Neumann bottleneck) 이라 부르는데, 이를 해결하기 위해 “메모리에 프로세서를 넣자!” (Process in Memory, PiM) 라는 해결책을 놓게 된다.

PiM은 어떤 메모리 소자에 넣는 것이 좋을까? 병목현상이 생길 때는 많은 데이터를 불러오거나 처리할 때 생기므로, 저장용량이 작은 메모리 소자에는 큰 성능 향상을 만들기 어려울 것이다. 대용량 저장 장치로는 가격과 대기전력면에서 가장 우수한 하드디스크 (Hard Disk Drive, HDD)가 있는데, 기본적으로 자성 도메인을 가지고 데이터를 저장한다. HDD는 head 가 기계적으로 회전하면서 데이터를 읽고 쓰는데, 이 부분에서 많은 에너지를 소모한다. 이를 전기적으로 바꾸고자 제안한 것이 ‘racetrack memory’ 이다. 기계적인 회전을 전류를 통한 자구벽 (Magnetic Domain Wall, DW) 이동으로 바꾸자는 아이디어인데, 소비전력 및 기계적 안정성 면에서 HDD 보다 우수할 것으로 예상하고 있다.

이러한 (전류 인가) DW 이동을 이용한 메모리에 프로세서를 설치하려면, 프로세서 역시 DW 이동을 통해 연산을 진행하는 것이 가장 좋을 것이다. 최근까지 스핀-궤도 토크 (spin-orbit torque, SOT) DW 이동을 통한 논리 연산은 제안 및 구현된 바 없으나, 본 연구 결과가 마무리 될 때쯤 ETH Zurich 에서 실험적으로 이를 구현했다는 보고가 나왔다 [1]. 아이디어가 거의 같아 참 아쉽지만, 해당 논문에서 조금 놓친 부분을 보충하여 논문을 작성할 수 있었다.

소자 동작을 이해하기 위해, 먼저 전류 인가 DW 이동에 대해 이해할 필요가 있다. 강자성체 (FM) – 중금속 (HM) 이종 접합 구조에서 중금속층 혹은 계면의 스핀류 (spin current) 가 자성층으로 유입되고 자화에 토크를 주게 되는데, 이것이 위에서 잠깐 이야기한 SOT 이다. 이 스핀 토크는 자성 제어에 꽤 효율적인 것으로 알려져 있어 많은 연구가 되고 있다. 이러한 토크는 자성 구조체인 DW 역시 움직일 수 있다는 것이 잘 알려져 있다.

한편 SOT 에 의한 DW 이동을 실현하려면 자성체에는 쟈로신스키-모리야 상호작용 (Dzyaloshinskii-Moriya Interaction, DMI) 이 있어야하고, 이 상호작용은 자성체가 특정 방향의 꼬인 구조를 에너지적으로 안정하게 만들어준다. 이러한 이유로, DMI 가 있는 상황에서 DW은 벽면에 수직인 방향 (Neél type)을 선호하게 된다. 이러한 현상은 수직 자기이방성을 낮춰 DW의 두께를 늘려도 계속 유지된다. 향후 편의를 위해 자성 띠 (magnetic wire) 방향을 x, 띠 두께 (wire width) 방향을 y, 필름 수직 방향을 z라고 하고, 이를 기준으로 편각 (polar angle) 및 방위각 (azimuthal angle) 을 정의하겠다. 즉 DMI 가 있는 상황에서, 수직 자구의 DW은 π/2 의 polar angle 을 가지고, 0 또는 π 의 azimuthal angle 을 가진다.

DW 반전기 (DW Inverter, NOT gate) 를 만들기 위해 가장 중요한 요소는 국소적으로 수평 자기이방성 (In-plane Magnetic Anisotropy, IMA)을 가지는 영역이 존재해야 한다는 것이다. IMA를 가진 영역을 가운데로 두고, 꼬인 구조를 선호하는 DMI로 인해, Up-Left-Down 혹은 Down-Right-Up 자구 구조가 에너지적으로 유리한 점을 가질 수 있다 [2]. 즉 Up(1)을 Down(0)으로, 0을 1로 바꿀 수 있는 구조라는 것이다! Input을 1에서 0, 또는 0에서 1로 바꾸는 switching을 DW 이동을 통해 할 수 있다는 사실과, switching 과정에서 output 이 연속적으로 바뀐다는 것을 (직접 코딩한) 미소 자기 전산모사 (micro-magnetic simulation)를 통해 확인할 수 있었다. [FIG.1]

당연한 이야기겠지만, 모든 소자에는 작동 범위가 존재한다. 이를 알아보기 위해, 본 연구에서는 소자에 인가하는 전류 밀도를 고정한 채로 wire width, IMA 영역 및 DMI strength 를 바꾸면서 소자 동작을 테스트하였다. 결과를 간단하게 요약하면, 소자의 DMI strength 가 주어지면 동작할 수 있는 IMA 영역의 길이가 거의 정해지고, 이 값이 커질수록 소자가 성공적으로 작동하는 IMA 길이의 범위가 넓어진다는 것이다. [FIG.2]

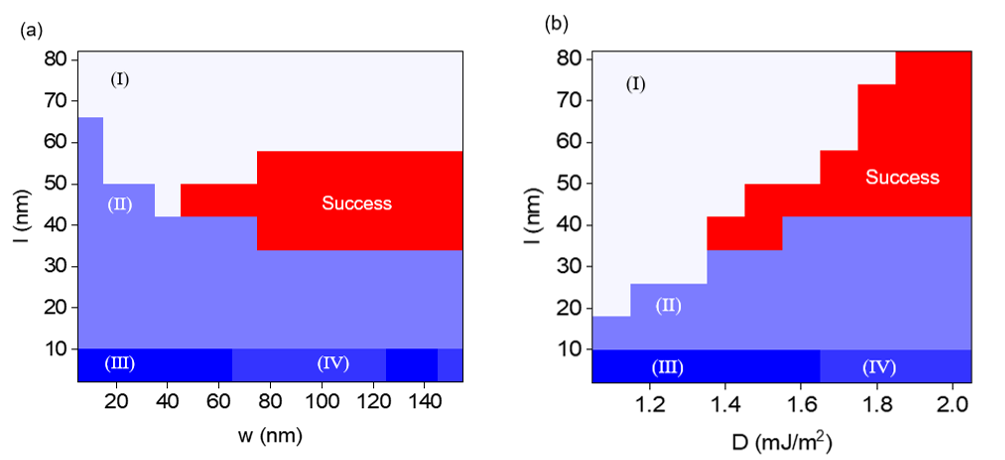
위의 작동 범위에 대한 연구를 토대로, 우리는 DW NOT gate 의 작동 원리를 파악할 수 있었다. 먼저 switching 을 위해 DW이 생기고, SOT에 의해 이동을 한다. 이동을 하다가 IMA 영역에 도달하면, SOT는 DW을 밀려고 하고, DMI는 꼬인 구조 (Down-Right-Up-Left-Down)를 유지하려고 하며, 정자기 상호작용 (magneto-static interaction)은 수직 자구가 IMA 영역에 들어오는 것을 막으려 한다. 이러한 상호작용의 competition이 임계 구동 전류를 결정한다. 이후 수직 자구가 IMA 영역에 들어오면 IMA 내에서 DW을 형성하는데, DMI 와 magneto-static interaction 에 의해서 DW 자화는 0 과 π/2 사이의 polar angle 을 갖는다. IMA 영역이 길어서 DMI 가 상대적으로 약해지게 되면 DW 자화는 π/2 에 가까운 polar angle 및 azimuthal angle 을 갖게 되고, 이는 SOT로 자화에 효율적인 토크를 주지 못함을 뜻한다. 즉 넓은 IMA 영역에서는 해당 영역에 생긴 DW을 밀지 못해서 동작이 불가능해진다. 이러한 사실을 종합해 볼 때, NOT gate 동작을 위해서 (i) DW을 IMA에 넣는 것, (ii) IMA 영역에서 DW 이동이 가능하게 하는 것 두가지가 중요하다는 것을 알 수 있다.

일반적인 논리학 이론에서, NAND 및 NOR 소자만으로 모든 Boolean logic 을 만들어 낼 수 있다는 사실은 잘 알려져 있다. 그래서 NAND 및 NOR 소자를 만드는 것이 중요한데, NOT gate 2개를 붙여서 reconfigurable NAND, NOR 소자를 만들 수도 있다는 것을 전산모사를 통해 증명하였다. 소자 모양은 아래 그림 [FIG.3]과 같은데, (1,0) 혹은 (0,1) input 이 들어오면 한 방향의 chirality 를 유지할 수 없다. 그래서 이러한 대칭성을 깰 수직 방향의 편향 자기장 (bias magnetic field) 가 소자 동작에 필요하다. 이 bias field 의 방향이 윗 방향일 때는 NOR gate, 아랫 방향일 때는 NAND gate 로써 동작한다.

위에서 설명한 것들이 논문의 주요 내용이고, 소비 전력은 어느정도, bias magnetic field 나 국소적인 IMA를 어떻게 바꾸어야 하는 것들은 논문의 마지막 부분에 언급이 되어 있다. 자세한 내용은 논문을 참고하기를 바란다.

결과적으로 ETH Zurich 의 Gambardella 그룹에서 (실험까지 다 해서) 논문이 먼저 나와 아쉬웠지만, 남는 것이 아주 없지는 않았다. DW motion에 대한 공부도 많이 되었고, 국내 및 PCT 국제 특허에 출원도 된 상태 (10-2020-0011870 & PCT/KR2020/006967, ‘자구벽 논리소자 및 이의 제조방법’)이며, Journal of Magnetics 에 표지논문으로 개제가 되어서 불행 중 다행이라 생각한다. 마지막으로, 연구를 같이 진행한 교수님과, 도움을 주신 많은 분들께 감사의 인사를 전하며 해설을 마치도록 하겠다.

저자 이근희
E-mail : [email protected]